Výpočet vzdialenosti Zem–Slnko z prechodu Venuše
Úloha
Meranie vzdialenosti Zem – Slnko z pozorovania prechodu Venuše dvoch miest ležiacich na rovnakom poludníku. Túto vzdialenosť je možné počítať aj pre miesta s rozdielnymi dĺžkami, no tento postup je matematicky omnoho náročnejší. Uvedieme veľmi zjednodušenú metódu založenú na prvých pozorovaniach z 18. storočia.
Zjednodušenia
Aby bola metóda prístupná aj študentom druhého stupňa zjednodušíme:
a. pozorovacie miesta, ich projekcia na povrch Slnka a stredy Zeme, Slnka a Venuše sú v jednej rovine,
b. obežné dráhy Zeme a Venuše okolo Slnka sú kružnice.
Základy
Predpokladáme, že študenti poznajú:
1. Matematické základy
a. Súčet uhlov v trojuholníku je 180 stupňov.
b. Pytagorova veta.
c. Definícia sínusovej funkcie.
2. Astronomické základy
a. Tretí Keplerov zákon.
b. Definícia horizontálnej paralaxy.
Úvod
Sir Edmund Halley odporúčal pozorovacie kampane na prechod Venuše v rokoch 1761 a 1769 a Jean–Nicolas Delisle všetky výsledky zhromaždil. Na výpočet vzdialenosti Zeme od Slnka použijeme skutočne namerané hodnoty zjednodušenou metódou pre pozorovateľov na tom istom poludníku. Pozorovatelia mali byť v rôznych zemepisných šírkach tak ďaleko, ako to len bolo možné, aby sa zlepšila presnosť výpočtu. Vybrané miesta boli často veľmi vzdialené, cestovanie bolo v tom čase nebezpečné, hrozili búrky a vojny medzi národmi, v Indickom oceáne bojovali Angličania a Francúzi. Zdôrazňujeme to preto, lebo na pozorovanie prechodu v roku 1761 boli prvýkrát vysielané vedecké expedície, ktorých bolo vyše 130 po celom svete. V roku 1769, boli pozorovatelia v Pondichery v Madrase, v Saint Domingo v západnej Indii, del Cabo in Baja California, v Hudsonovom zálive v Kanade, v Papeete na Tahiti, vo Vardö v Laponsku, v Cajanebourgu na polostrove Kola a v Jakutsku na Sibíri. Spolu to bolo 151 pozorovateľ na 77 rozdielnych miestach. Výpravy boli veľmi rozdielne a niektoré výsledky nesplnili očakávania!
Pozorovania zo Zeme
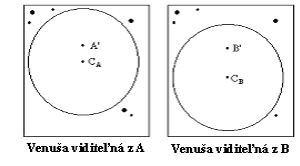
Predpokladajme dvoch pozorovateľov na Zemi, ktorí sú na miestach A a B na rovnakom poludníku (meridiáne), ale vo veľmi rozdielnych zemepisných dĺžkach. Venuša je z týchto miest viditeľná ako malý tmavý disk na Slnku v dvoch polohách A' a B', pretože priamky medzi miestami A a B a Venušou sú rozdielne.
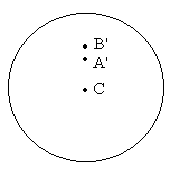
Spojením oboch pozorovaní a použitím referenčných hviezd môžeme merať paralaktický posun. Je nutné prekryť oba obrazy Slnka (C) a vzdialenosť A' a B' je vzdialenosť medzi dvomi polohami Venuše pozorovanými v rovnakom čase z miest A a B.
Ak pozorujeme pohyb Venuše počas celého prechodu, zaznamenáme celé pozorovanie. Ak pozorujeme z miest A a B, dostaneme dve rovnobežky, každú pre jedno pozorovacie miesto. Vzdialenosť medzi týmito čiarami je paralaktický posun Db.
Ako zmerať vzdialenosť Zem - Slnko
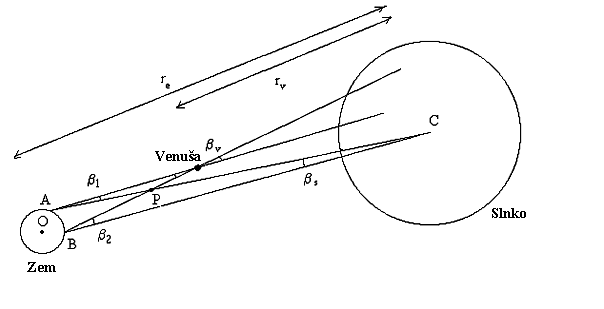
Máme rovinu definovanú tromi bodmi: stred Zeme O, stred Slnka C a stred Venuše V. Ak sú dvaja pozorovatelia na rovnakom poludníku v miestach A a B, ich obrazy Venuše sa javia na povrchu Slnka ako body A' a B'.
Trojuholníky APV a BPC majú v P rovnaké vonkajšie uhly a tiež ich súčet je rovnaký
bv + b1 = bs + b2
preto
bv – bs = b2 – b1 = Db
Db je uhol medzi rozdielnymi polohami Venuše na slnečnom disku. Poslednú rovnicu upravíme
Db = bs ((bv / bs) – 1)
Nech je re vzdialenosť Zem - Slnko a rv vzdialenosť Venuša – Slnko,
potom paralaxa Venuše je bv = AB / (re– rv),
paralaxa Slnka je bs = AB / re a podiel je bv / bs = re / (re– rv).
Rovnicu upravíme nasledovne
Db = bs ((re / (re– rv)) – 1) = bs rv / (re– rv)
Môžeme teda určiť slnečnú paralaxu
bs = Db ((re / rv) – 1)
Všimnite si, že Db je paralaktický posun, teda vzdialenosť medzi oboma priamkami. Pomer rv / re môžeme vypočítať použitím tretieho Keplerovo zákona, pretože poznáme obežnú dobu Venuše 224,7 dní a obežnú dobu Zeme 365,25 dní
(re/rv)3 = (365,25/224,7)2
preto
re/rv = 1,38248
Tento výsledok použijeme vo vzorci pre paralaxu a dostaneme
bs = Db ((re / rv) – 1) = Db (1,38248 – 1)
potom
bs = 0,38248 Db
Konečne použitím vzorca pre definíciu paralaxy určíme vzdialenosť Zeme od Slnka re ako
re = AB / bs
Potrebujeme teda poznať vzdialenosť AB medzi pozorovacími miestami a zmerať Db z pozorovania prechodu.
Pozorovania v roku 1769
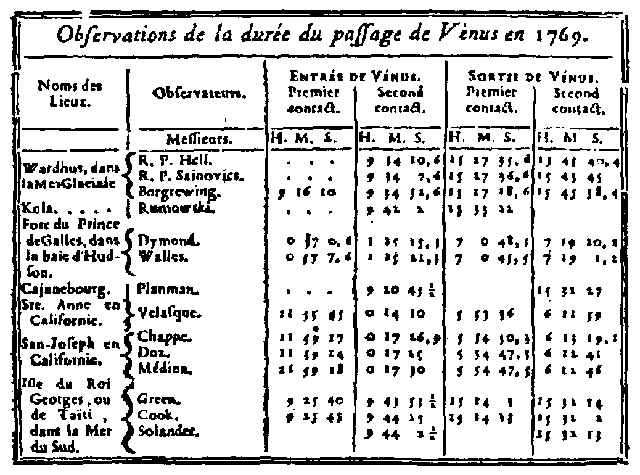
Údaje sú časy kontaktov pozorované z rôznych miest, kresba prechodov v rokoch 1761 a 1769 je publikovaná v „A History of Astronomy“ od A. Pannekoeka.
Pre výpočet budeme používať výsledky z roku 1769 z Vardö (priamka 3) a Tahiti (priamka 1).
1) Vzdialenosť medzi pozorovateľmi v miestach A a B
Vzdialenosť AB môže byť určená zo zemepisnej šírky oboch pozorovacích miest. Na obrázku j1 and j2 sú zemepisné šírky miest A a B, R je polomer Zeme.
Pre trojuholník RAB platí
sin ((j1 + j2) / 2) = (AB / 2) / R
Vzdialenosť AB je
AB = 2 R sin ((j1 + j2) / 2)
Musíme si uvedomiť: ak sú obe miesta na tej istej pologuli je uhol (j1 – j2) / 2 ale geometrická situácia sa zmení ak miesta majú rozdielne dĺžky.
Vardö (Laponsko) a Papeete (Tahiti) sú na rovnakom poludníku (meridiáne) a ich zemepisné šírky sú 70° 21' N a 17° 32' S. Vo Vardö bolo Slnko pozorované okolo polnoci (polnočné Slnko).
Z geometrie určíme nový uhol, ktorý je
j = (90 – j1) + 90 + j2 = 127º 11'
a ak budeme počítať s polomerom Zeme R = 6378 km, dostaneme
AB = 2 R sin(j / 2) = 11 425 km
2) Vzdialenosť Db medzi dvoma pozorovanými dráhami Venuše
Aby sme mohli vypočítať Db, musíme zmerať priemer Slnka D a vzdialenosť Db medzi oboma dráhami, teda A'B' na kresbe alebo fotografii. Uhlový priemer Slnka zo Zeme je 30' a teda
Db/30' = A'B' / D
Db = (30')(A'B' / D)
ale vo vzorci potrebujeme uhlový rozmer Slnka v radiánoch, preto
Db = (30 p; / 10800) (A'B' / D)
Db = (p; /360) (A'B' / D)
Zmeriame teda vzdialenosť medzi priamkou 1 a 3 a dostaneme Db = 1,5 mm , priemer slnečnej kresby D = 70 mm. Preto
Db = (p/360)(1,5/70) = 0,00019 radiánov
Ak meriame Db priamo, dopúšťame sa chyby, pretože zmerať takúto malú vzdialenosť medzi dvoma priamkami je problematické. Pomocou Pytagorovej vety to však môžeme urobiť presne.
Použitím vzťahu pre paralaxu máme
bS = 0,38248 Db
a pre slnečnú paralaxu, vzdialenosť Zeme od Slnka
re = AB / bs
Použitím údajov z roku 1769 vypočítame re
re = 157.106 km
Ako je známe, vzdialenosť Slnka od Zeme je re = 149,6.106 km. Aby sme získali presnejší výsledok, museli by sme presnejšie určiť Db.
Tretí Keplerov zákon
Tretí Keplerov zákon hovorí, že veľké poloosy eliptických dráh Venuše a Zeme av, ae a doby obehu Tv a Te sú vo vzťahu
(ae / av)3 = (Te /Tv)2
Keďže sme zjednodušili, že dráhy sú kruhové, potom platí vzťah
(re/ rv)3 = (Te /Tv)2
Paralaxa Slnka (horizontálna paralaxa)
Paralaxa Slnka je definovaná ako uhol b
V trigonometrii je sin b = R / r, ale uhol b je malý, a tak sin b môžeme v radiánoch nahradiť b. R je polomer Zeme a r je vzdialenosť Zeme. Pre výpočet použijeme vzťah
r = R / b.
Výpočet Db meraním tetív
Vzdialenosť Db medzi tetivami A a B je merateľen ťažko, pretože vzhľadom na priemer obrazu Slnka sú veľmi blízko pri sebe. Meranie vzdialenosti A'B' môžeme nahradiť meraním tetív A1A2 a B1B2, ktoré sú dráhami Venuše na slnečnom disku pre pozorovateľov A a B.
Použitím Pytagorovej vety dostaneme:
B'S = ½√(D2 – B1B22)
A'S = ½√(D2 – A1A22)
Aby sme určili A'B', vypočítame rozdiel B'S – A'S
A'B' = ½[√(D2 – B1B22) – √(D2 – A1A22)]
Delením priemerom D dostaneme
A'B' / D = ½[√(1 – (B1B2 / D)2) – √(1 – (A1A2 / D)2)]
Meraním A1A2, B1B2 a D na obraze Slnka dostaneme, A1A2 = 52 mm (čiara 3), B1B2 = 49 mm (čiara) a D = 70 mm. Potom
A'B' / D = ½[√(1 – (49/70)2) – √(1 – (52 / 70)2)] = 0,02235
a Db bude
Db = (31 p / 360) 0,02235 = 0,00020 radiánov
Použitím vzorca pre paralaxu dostaneme
bs = 0,38248 Db
a použitím vzorca pre paralaxu Slnka vzdialenosť Zeme od Slnka re je
re = AB / bs
Použitím údajov z expedícií v roku 1769 a AB = 11 425 km vypočítame
re = 149 . 106 km
Vidíme, že dosiahnuť použiteľné výsledky je ťažké napriek tomu, že výsledok je relatívne blízko skutočnej hodnote.
Meranie vzdialenosti Zem – Slnko z pozorovania prechodu Venuše dvoch miest ležiacich na rovnakom poludníku. Túto vzdialenosť je možné počítať aj pre miesta s rozdielnymi dĺžkami, no tento postup je matematicky omnoho náročnejší. Uvedieme veľmi zjednodušenú metódu založenú na prvých pozorovaniach z 18. storočia.
Zjednodušenia
Aby bola metóda prístupná aj študentom druhého stupňa zjednodušíme:
a. pozorovacie miesta, ich projekcia na povrch Slnka a stredy Zeme, Slnka a Venuše sú v jednej rovine,
b. obežné dráhy Zeme a Venuše okolo Slnka sú kružnice.
Základy
Predpokladáme, že študenti poznajú:
1. Matematické základy
a. Súčet uhlov v trojuholníku je 180 stupňov.
b. Pytagorova veta.
c. Definícia sínusovej funkcie.
2. Astronomické základy
a. Tretí Keplerov zákon.
b. Definícia horizontálnej paralaxy.
Úvod
Sir Edmund Halley odporúčal pozorovacie kampane na prechod Venuše v rokoch 1761 a 1769 a Jean–Nicolas Delisle všetky výsledky zhromaždil. Na výpočet vzdialenosti Zeme od Slnka použijeme skutočne namerané hodnoty zjednodušenou metódou pre pozorovateľov na tom istom poludníku. Pozorovatelia mali byť v rôznych zemepisných šírkach tak ďaleko, ako to len bolo možné, aby sa zlepšila presnosť výpočtu. Vybrané miesta boli často veľmi vzdialené, cestovanie bolo v tom čase nebezpečné, hrozili búrky a vojny medzi národmi, v Indickom oceáne bojovali Angličania a Francúzi. Zdôrazňujeme to preto, lebo na pozorovanie prechodu v roku 1761 boli prvýkrát vysielané vedecké expedície, ktorých bolo vyše 130 po celom svete. V roku 1769, boli pozorovatelia v Pondichery v Madrase, v Saint Domingo v západnej Indii, del Cabo in Baja California, v Hudsonovom zálive v Kanade, v Papeete na Tahiti, vo Vardö v Laponsku, v Cajanebourgu na polostrove Kola a v Jakutsku na Sibíri. Spolu to bolo 151 pozorovateľ na 77 rozdielnych miestach. Výpravy boli veľmi rozdielne a niektoré výsledky nesplnili očakávania!
Pozorovania zo Zeme
Predpokladajme dvoch pozorovateľov na Zemi, ktorí sú na miestach A a B na rovnakom poludníku (meridiáne), ale vo veľmi rozdielnych zemepisných dĺžkach. Venuša je z týchto miest viditeľná ako malý tmavý disk na Slnku v dvoch polohách A' a B', pretože priamky medzi miestami A a B a Venušou sú rozdielne.
|
Spojením oboch pozorovaní a použitím referenčných hviezd môžeme merať paralaktický posun. Je nutné prekryť oba obrazy Slnka (C) a vzdialenosť A' a B' je vzdialenosť medzi dvomi polohami Venuše pozorovanými v rovnakom čase z miest A a B.
|
Ak pozorujeme pohyb Venuše počas celého prechodu, zaznamenáme celé pozorovanie. Ak pozorujeme z miest A a B, dostaneme dve rovnobežky, každú pre jedno pozorovacie miesto. Vzdialenosť medzi týmito čiarami je paralaktický posun Db.
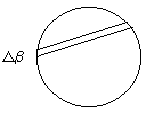
|
Ako zmerať vzdialenosť Zem - Slnko
Máme rovinu definovanú tromi bodmi: stred Zeme O, stred Slnka C a stred Venuše V. Ak sú dvaja pozorovatelia na rovnakom poludníku v miestach A a B, ich obrazy Venuše sa javia na povrchu Slnka ako body A' a B'.
|
Trojuholníky APV a BPC majú v P rovnaké vonkajšie uhly a tiež ich súčet je rovnaký
bv + b1 = bs + b2
preto
bv – bs = b2 – b1 = Db
Db je uhol medzi rozdielnymi polohami Venuše na slnečnom disku. Poslednú rovnicu upravíme
Db = bs ((bv / bs) – 1)
Nech je re vzdialenosť Zem - Slnko a rv vzdialenosť Venuša – Slnko,
potom paralaxa Venuše je bv = AB / (re– rv),
paralaxa Slnka je bs = AB / re a podiel je bv / bs = re / (re– rv).
Rovnicu upravíme nasledovne
Db = bs ((re / (re– rv)) – 1) = bs rv / (re– rv)
Môžeme teda určiť slnečnú paralaxu
bs = Db ((re / rv) – 1)
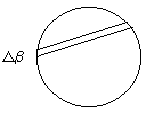
|
Všimnite si, že Db je paralaktický posun, teda vzdialenosť medzi oboma priamkami. Pomer rv / re môžeme vypočítať použitím tretieho Keplerovo zákona, pretože poznáme obežnú dobu Venuše 224,7 dní a obežnú dobu Zeme 365,25 dní
(re/rv)3 = (365,25/224,7)2
preto
re/rv = 1,38248
Tento výsledok použijeme vo vzorci pre paralaxu a dostaneme
bs = Db ((re / rv) – 1) = Db (1,38248 – 1)
potom
bs = 0,38248 Db
Konečne použitím vzorca pre definíciu paralaxy určíme vzdialenosť Zeme od Slnka re ako
re = AB / bs
Potrebujeme teda poznať vzdialenosť AB medzi pozorovacími miestami a zmerať Db z pozorovania prechodu.
Pozorovania v roku 1769
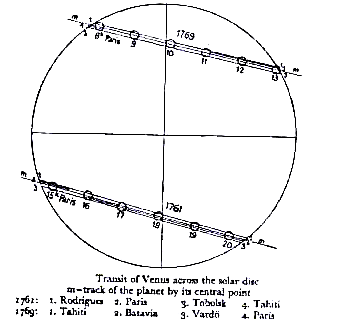
Údaje sú časy kontaktov pozorované z rôznych miest, kresba prechodov v rokoch 1761 a 1769 je publikovaná v „A History of Astronomy“ od A. Pannekoeka.
|
|
Pre výpočet budeme používať výsledky z roku 1769 z Vardö (priamka 3) a Tahiti (priamka 1).
1) Vzdialenosť medzi pozorovateľmi v miestach A a B
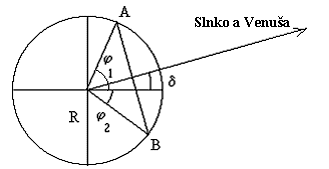
Vzdialenosť AB môže byť určená zo zemepisnej šírky oboch pozorovacích miest. Na obrázku j1 and j2 sú zemepisné šírky miest A a B, R je polomer Zeme.
|
Pre trojuholník RAB platí
sin ((j1 + j2) / 2) = (AB / 2) / R
Vzdialenosť AB je
AB = 2 R sin ((j1 + j2) / 2)
Musíme si uvedomiť: ak sú obe miesta na tej istej pologuli je uhol (j1 – j2) / 2 ale geometrická situácia sa zmení ak miesta majú rozdielne dĺžky.
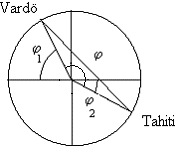
Vardö (Laponsko) a Papeete (Tahiti) sú na rovnakom poludníku (meridiáne) a ich zemepisné šírky sú 70° 21' N a 17° 32' S. Vo Vardö bolo Slnko pozorované okolo polnoci (polnočné Slnko).
|
Z geometrie určíme nový uhol, ktorý je
j = (90 – j1) + 90 + j2 = 127º 11'
a ak budeme počítať s polomerom Zeme R = 6378 km, dostaneme
AB = 2 R sin(j / 2) = 11 425 km
2) Vzdialenosť Db medzi dvoma pozorovanými dráhami Venuše
Aby sme mohli vypočítať Db, musíme zmerať priemer Slnka D a vzdialenosť Db medzi oboma dráhami, teda A'B' na kresbe alebo fotografii. Uhlový priemer Slnka zo Zeme je 30' a teda
Db/30' = A'B' / D
Db = (30')(A'B' / D)
ale vo vzorci potrebujeme uhlový rozmer Slnka v radiánoch, preto
Db = (30 p; / 10800) (A'B' / D)
Db = (p; /360) (A'B' / D)
Zmeriame teda vzdialenosť medzi priamkou 1 a 3 a dostaneme Db = 1,5 mm , priemer slnečnej kresby D = 70 mm. Preto
Db = (p/360)(1,5/70) = 0,00019 radiánov
Ak meriame Db priamo, dopúšťame sa chyby, pretože zmerať takúto malú vzdialenosť medzi dvoma priamkami je problematické. Pomocou Pytagorovej vety to však môžeme urobiť presne.
Použitím vzťahu pre paralaxu máme
bS = 0,38248 Db
a pre slnečnú paralaxu, vzdialenosť Zeme od Slnka
re = AB / bs
Použitím údajov z roku 1769 vypočítame re
re = 157.106 km
Ako je známe, vzdialenosť Slnka od Zeme je re = 149,6.106 km. Aby sme získali presnejší výsledok, museli by sme presnejšie určiť Db.
Tretí Keplerov zákon
Tretí Keplerov zákon hovorí, že veľké poloosy eliptických dráh Venuše a Zeme av, ae a doby obehu Tv a Te sú vo vzťahu
(ae / av)3 = (Te /Tv)2
Keďže sme zjednodušili, že dráhy sú kruhové, potom platí vzťah
(re/ rv)3 = (Te /Tv)2
Paralaxa Slnka (horizontálna paralaxa)
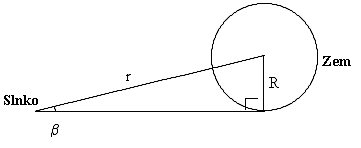
Paralaxa Slnka je definovaná ako uhol b
|
V trigonometrii je sin b = R / r, ale uhol b je malý, a tak sin b môžeme v radiánoch nahradiť b. R je polomer Zeme a r je vzdialenosť Zeme. Pre výpočet použijeme vzťah
r = R / b.
Výpočet Db meraním tetív
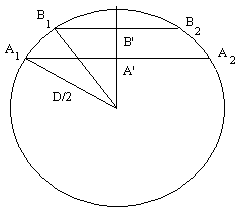
Vzdialenosť Db medzi tetivami A a B je merateľen ťažko, pretože vzhľadom na priemer obrazu Slnka sú veľmi blízko pri sebe. Meranie vzdialenosti A'B' môžeme nahradiť meraním tetív A1A2 a B1B2, ktoré sú dráhami Venuše na slnečnom disku pre pozorovateľov A a B.
|
Použitím Pytagorovej vety dostaneme:
B'S = ½√(D2 – B1B22)
A'S = ½√(D2 – A1A22)
Aby sme určili A'B', vypočítame rozdiel B'S – A'S
A'B' = ½[√(D2 – B1B22) – √(D2 – A1A22)]
Delením priemerom D dostaneme
A'B' / D = ½[√(1 – (B1B2 / D)2) – √(1 – (A1A2 / D)2)]
Meraním A1A2, B1B2 a D na obraze Slnka dostaneme, A1A2 = 52 mm (čiara 3), B1B2 = 49 mm (čiara) a D = 70 mm. Potom
A'B' / D = ½[√(1 – (49/70)2) – √(1 – (52 / 70)2)] = 0,02235
a Db bude
Db = (31 p / 360) 0,02235 = 0,00020 radiánov
Použitím vzorca pre paralaxu dostaneme
bs = 0,38248 Db
a použitím vzorca pre paralaxu Slnka vzdialenosť Zeme od Slnka re je
re = AB / bs
Použitím údajov z expedícií v roku 1769 a AB = 11 425 km vypočítame
re = 149 . 106 km
Vidíme, že dosiahnuť použiteľné výsledky je ťažké napriek tomu, že výsledok je relatívne blízko skutočnej hodnote.
